Probability Theory

Abstract

This lecture overviews Probability Theory  that has many applications in a multitude of scientific and engineering disciplines, notably in Pattern Recognition and Machine Learning. It covers the following topics in detail: 

1. Probability Space, Bayes theorem.
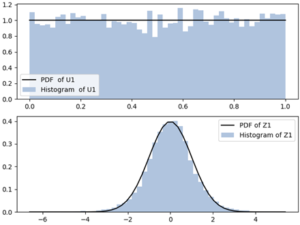
2. One random variable, cumulative probability functions, probability density functions, expectation operators, mean, variance, functions of random variables, normal, uniform, Laplacian distributions.
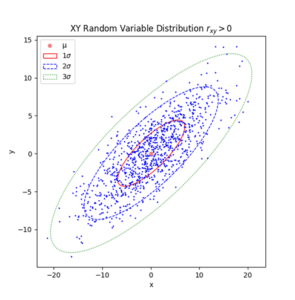
3. Two random variables, joint cumulative probability functions, joint probability density functions, expectation operators, independence, correlation coefficient, functions of two random variables, 2D normal, uniform, Laplacian distributions.
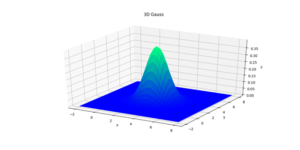
4. Multiple Random Variables, random vectors, joint cumulative probability functions, joint probability density functions, expectation operators, independence, correlation matrix, covariance matrix, functions of two random variables, multivariate normal distributions.

Finally, a section is devoted on random number and random vector generation.